Average Calculator
Average Calculator
Our average calculator can calculate the average for the given data set in no time at all. You just have to insert the value in the given input box and press the “Calculate” button. It will instantly provide the average value, sum value, and average count (total number of items).
This average value calculator has two tabs. There is a reason behind the two-tab view. The first tab is named “Single Value” tab. It has a single input box where all the values can be entered separated by commas. It is necessary to separate the values by commas. Otherwise, it will not give you the best results. On the other hand, if you need to enter a separate value, then the “Multiple Input” tab will meet your requirements.
The multiple input tab has six input boxes by default, and more input boxes can be added by clicking on the “Add more fields” button. Users can add as many input boxes as needed to calculate the average of his/her data set. These added input boxes can also be deleted by using a tiny red button against each input box. Our average finder tool has the perfect accuracy and speed to meet the requirements of today’s fast paces working environment.
What is Average?
Average has several meanings in different contexts. In mathematics, it is a central value that represents a group of data to comprehend the overall value of the presented data. It is calculated by adding all the values of the given data and dividing the result of the sum by the total number of values in the data set. Let’s understand it by a simple example.
Suppose a student got 40 marks in Physic, 50 in Mathematics, 55 in Chemistry, and 60 in English. All of the courses consist of 100 marks per course. What will be the average marks of the student?
To compute the average marks of the student, first, we have to add all the marks obtained.
40 + 50 + 55 + 60 = 205
The total obtained marks are 205, out of 400. There are total of 4 courses. So, we will divide 205 with 4 to get the average marks. By dividing, we get:
205/4 = 51.25
So, the average marks of the student are 51.25. We can deduce that the student obtained 51.25 marks per course. The average gave us a general overview of the performance of the student.
Types of Average
There are three types of average. Mean, Median, and Mode. We will briefly discuss the types of average to get a good understanding of average.
-
Mean or Arithmetic mean
The mean, which is also known as the arithmetic mean, is the central value, which is estimated to evaluate the central value of a given set of data. This mathematical measurement is the most commonly used average and is usually called mean in daily life.
The sum of all the values in a data set is computed to calculate the arithmetic mean. The sum of the values then divided by the total number of values in the data.
The arithmetic mean should be used if a data set includes values that are not extremely high or low and are reasonably equally spread.
The formula for the mean
Although the mathematical formula is not relevant for calculating the mean, it may be useful to know the basic formula to calculate the arithmetic mean. The arithmetic mean can be calculated by using the formula below.
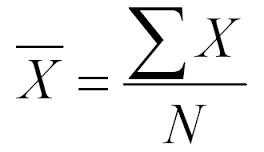
In this arithmetic mean equation, x̅ refers to the arithmetic mean and read as X bar. Σ is referred to as sigma, and it is a Greek word that represents the term “sum.” The X represents every single value in the data set, and N is the total number of values. This formula can be described as: the arithmetic mean is equal to the sum of each value divided by the total number of participants in the data set.
-
Median
Median is another type of average that is most commonly used after arithmetic mean. It is the middle value in a sorted data set. Values are sorted in higher to lower order or in lower to higher order to calculate the median. Median varies according to the total number of values in the data set.
If the total number of values in given data is even, for example, {2, 4, 6, 8 10}, we will calculate the median by excluding a value from each side of the data set. The remaining value will be median, which is 6 in this data set is.
If the total number of values is odd in a data set, for example, {2, 4, 6, 8, 10, 12}, we will calculate the median the same way, but there will be two values in the end. In this case, those two values are 6 and 8. Simply add 6 and 8 and divide by 2 to get the median. In this example, 7 is the median.
Median Formula
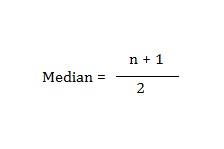
-
Mode
The mode is a type of average that is calculated based on the frequency of the values. A value is considered as a mode in a data set if it occurs more often than any other value. In simple words, a mode is the most repeated value in a given data set.
For example, in data set {2, 4, 6, 7, 7, 8, 8, 0, 5}, 7 and 8 are repeating two times, which is more than any other value. So the mode in this data set is both 7 and 8. This method can be used to calculate mode in an ungrouped data set. For grouped data, a formula is used to evaluate mode.
Mode Formula
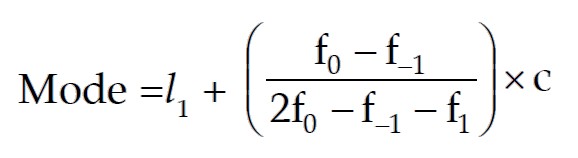
Applications of average
The average is used in every field of life frequently. It is used by students, teachers, shopkeepers, business people, engineers in their daily routine. It would not be wrong that almost every person uses average in their life at some stage.
You may hear on a news channel that people spend an average of 12 hours of their time per day on their mobile phones. It does not mean that every single person is spending 12 hours on a mobile phone.
This average may be calculated based on a data set collected from specific areas and people to get an idea of how many hours people spend on their phones. Some may use their phone for 4 hours, some for six, or some for 15 hours.
The data is always varying when calculating the average, but it gives us a general overview of the usage of mobile phones by users. This example is very simple, and in the same way, the average is used to summarize big numbers and data into a single number.