Arithmetic Sequence Calculator
Our online arithmetic calculator is an online tool that evaluates the number sequence, generated by inserting a constant value. It can be used to locate any sequence property such as the common difference, the first term, the number of the first n terms, or nth term.
Arithmetic sequence calculator is also known as an arithmetic series calculator.
What is Arithmetic Sequence?
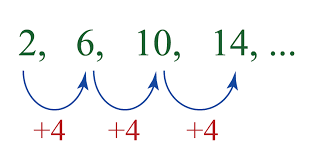
An arithmetic sequence is a sequential representation of numbers in which the difference is always the same in each term. This difference can be positive or negative, and depending on the sign will lead to a positive or negative infinity sequence.
Few examples:
2, 4, 6, 8, 10, 12, 14, 16…
5, 2, -1, -4, -7, -10, -13, -16...
60, 60.1, 60.2, 60.3, 60.4, 60.5...
The sequence is called an increasing sequence if the common difference of an arithmetic series is positive. It will be called a decreasing sequence if the common difference is negative. If the common difference is zero, it will be a monotone sequence.
Arithmetic sequence formula
Formula to find sum of arithmetic sequence/progression is:
S = n/2 × [2a₁ + (n - 1)d]
Formula to find nth term is:
an = a + (n - 1)d
In this equation,
a₁ is the first term of the sequence,
an is the nᵗʰ term of the sequence,
d is a common difference.
Let's find arithmetic sequence, its sum & nth term
Calculate nth term and sum of arithmetic progression if there are 10 number of terms with first term of 3 and difference of 6
Sum of arithmetic progression/sequence
S = n/2 × [2a₁ + (n - 1)d]
S = 10/2 × [2(3) + (10 - 1) × 6]
S = 300
Nth term
an = a + (n - 1)d
an = 3 + (10 - 1) × 6
an = 57
Arithmetic Sequence
To get arithmetic sequence, simply add common difference in first term. Then keep adding common difference in the previous number until you get the final number in sequence.
a1 = 3
a2 = a1 + d = 3 + 6 = 9
a3 = a2 + d = 9 + 6 = 15
a4 = a3 + d = 15 + 6 = 21
a5 = a4 + d = 21 + 6 = 27
a6 = a5 + d = 27 + 6 = 33
a7 = a6 + d = 33 + 6 = 39
a8 = a7 + d = 39 + 6 = 45
a9 = a8 + d = 45 + 6 = 51
a10 = a9 + d = 51 + 6 = 57
So, the sequence will be,
9, 15, 21, 27, 33, 39, 45, 51, 57