Standard Deviation Calculator
Standard Deviation Calculator
What is Standard Deviation?
Standard deviation means a measure of how much a set of values is changed or dispersed. A high value suggests that values are split across a broader range, while a low values shows that values are close to the arithmetic mean. It is represented by sigma (σ) for population and by letter s for a sample data, which is a Greek letter.
The standard deviation of a population, arbitrary variable, prospect distribution, or data set is the square root of variance of itself. The standard deviation of a population and the standard error of a piece of data originating from that specific population is quite distinct but is correlated with the inverse of the square root of the number of observations.
It can be used in different scenarios and equations like most of the statistical and mathematical practical work. Besides, it is used to measure statistical results, such as margin of error, in addition to expressing population variability.
Population Standard Deviation
The population standard deviation is denoted by σ and is used for measuring the SD for a whole population. It is calculated by taking the square root of the variance of the data set. The following population standard deviation formula can be used for the dataset of an entire population.
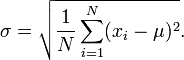
μ is the mean value,
∑ is the sum of values,
N is the total number of values in data set, and xi is an individual value.
Sample standard deviation Formula
In many cases, each individual within the population cannot be sampled, and the above equation needs to be modified to measure the standard deviation via random sampling of the surveyed population. The sample standard deviation is a general estimate of the population standard deviation, typically denoted by s. There are several sample standard deviation equations to calculate the sample standard deviation because there is not one consistent estimator that is reliable and efficient. Sample standard deviation equation is:
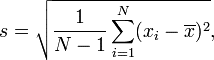
Where xi is one sample value from the sample data, N is the sample size, x̄ is the sample mean, and ∑ is the sum of values.
Standard Deviation Calculator
Our standard deviation calculator can calculate it in a blink of an eye. It is very simple and easy to use. Enter the data set in the input box and click the “Calculate” button to get the results. Standard deviation calculations are quick, and it calculates the results very precisely.
Our standard deviation calculator acts as a population standard deviation calculator, sample standard deviation calculator, and sample mean calculator as well. It provides a total of ten calculations for the given data set. These calculations include:
Count: It counts the number of values in a data set.
Sum: Calculates the sum of all values.
Sum of Differences2: Calculates the square of the sum of differences.
Population Variance: It estimates the population variance for the provided data set.
Population Standard Deviation: Calculates the population standard deviation for the entire population.
Sample Variance: It provides sample variance for a sample set of data.
Sample Standard Deviation: Also provides sample standard deviation for a sample set of values.
Differences: Calculates the difference by subtracting every number from the mean value.
Differences2: It also calculates the square of each difference.
Why use our Standard Deviation Calculator?
The calculation of standard deviation is a complicated task if you do it by yourself. Most of the statisticians use online standard deviation calculators to calculate the population and sample standard deviation as well as different variances. Our standard deviation calculator makes it easy for you to calculate population, sample, and relative standard deviation without getting stuck into the complex formulas.