Decimal to Octal Division
Decimal to Octal Division
There are multiple number systems with Octal and Decimal being two of them. Octal has base 8 and has values from 0 to 7. Similarly, the decimal system has base 10. The following video gives an insight of the conversion procedure.
Steps of conversion
The division method is a common one used for the decimal to octal conversion. Here are the steps involved
1. The decimal number and breakdown into powers of 8
Suppose that the number 84 in decimal format needs to be converted to the octal form. It would be written as
(84)10
Let us write down the powers of 8 until we reach a value greater than 84 is reached
|
80 |
0 |
|
81 |
8 |
|
82 |
64 |
|
83 |
512 |
The above table shows the powers of 8 in the left column and equivalent decimal values in the right column. We will only select the first three rows the decimal values are less than 84. The fourth row shows a decimal value of 512 so it will be ignored which is why it has been written in strike text
2. The division cycle
From the above step, we have the following extractions
80 = 1
81 = 8
82 = 64
Now, let us proceed to the stage of division. Here, we need to divide the initial number (84) by the maximum decimal value from the powers of 8 (in this case 64). This step is used to determine the number of octals present in a given decimal number. Here, we have to take all the powers of 8 which have an output lesser than the actual decimal digit. Thus, the first three which have a maximum value of 64 are taken into consideration.
84 / 64 gives a quotient of 1 and a remainder of 20. Let us reuse the outputs produced again and add this result.
- 80 = 1
- 81 = 8
- 82 = 64
- 84 / 64 (quotient of 1 and remainder of 20)
3. Going to the next power of 8 for division
From the above step, when 84 is divided by 64, we get a quotient of 1 and a reminder sum of 20. Now, moving on, the remainder with each division step will be divided by a smaller power of 8. This process will be repeated until there is no remainder left.
In the first step, 84 was divided by 64 which is 82 (eight raised to the power 2). Now, we would use one smaller power of 8. Thus, in mathematical terms we have.
- Remainder = 20
- 81 = 8
Now, when we divide 20 by 8, we will get a quotient of 2 and remainder of 4.
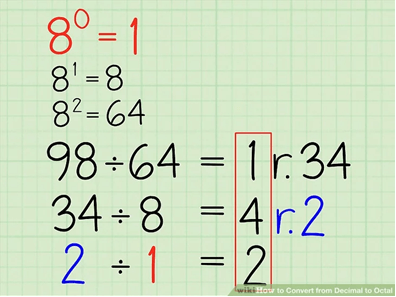
4. Reaching to remainder zero
The division process of converting octal to division is repeated until we reach a remainder of zero. This is when the conversion process will be completed. From the above step, we have a remainder of 4. A smaller power of 8 will be given as 80
Divide the remainder 4 by 80
4 / 1 gives a quotient of 4 and remainder of zero. This means that 4 is perfectly divisible by 1.
Let us redraw the steps followed for this octal to decimal conversion
- 80 = 1
- 81 = 8
- 82 = 64
- 84 / 64 (quotient of 1 and remainder of 20)
- 20 / 81 (quotient of 2 and remainder of 4)
- 4 / 80 (quotient of 4 and remainder of 0)
5. Pick all the quotients to get the converted form
If you have a good look at the extractions from step 4, we have performed three steps of division before reaching the remainder of 0. Each of these steps has a quotient.
- From step 1, the quotient is 1
- From step 2, the quotient is 2
- From step 3, the quotient is 4.
Now, write all the quotients together from the beginning to the end. Hence we will get the following converted form in octal.
(84)10 = (124)8
Thus, we can say that 84 in decimal form is equal to 124 on octal
6. Confirming the results
Even the best mathematicians make mistakes so checking the results is important. Here is how you can attain a confirmation.
The decimal value we started with was 84 and the converted octal number is 124. Now, let us perform the opposite of what we did in the division process. At that time, we divided the remainder with the corresponding power of 8. To check results, we will use multiplication.
The octal number is 124
- Multiply 1 with 82, result is 64
- Multiply 2 with 81, result is 16
- Multiply 4 with 80, result is 4
Now, let us add all the results
64 + 16 + 4 = 84. Hence, this means that we have performed the conversion without any errors as 84 was the original number in decimal form.

References